Data Extraction Evaluation
Matthew Leonawicz
Next steps
Combining sampling and data reduction methods while using the most efficient R functions can be particularly useful when processing large numbers of high-resolution geotiff raster layers. One thing I already do when extracting from many files by shapefile is I avoid extracting by shape more than once. I do it one time to obtain the corresponding raster layer cell indices. Then on all subsequent maps I extract by cell indices which is notably faster. Ultimately, there is much more room for speed improvements in terms of efficient use of statistics than in strictly programmatic corner-cutting.
The plots below benchmark different sample mean computations. Comparisons involve the sample mean of the entire data set and do not involve the main approach outlined above which focuses on efficiency gains by taking the mean of a smaller, representative sample. This provides some insight into how it is beneficial nonetheless to considering the right programmatic approach in conjunction with statistical efficiencies.
## Unit: milliseconds
## expr min lq mean median
## mean(v, na.rm = T) 329.44610 330.05676 335.42389 330.57520
## mean(v[dat.ind]) 13.95565 14.04958 15.29547 14.12624
## sum(v[dat.ind])/nd 12.42334 12.51275 14.71309 12.59486
## .Internal(mean(v[dat.ind])) 13.87759 13.97556 16.08770 14.05844
## .Primitive("sum")(v[dat.ind])/nd 12.41090 12.51306 14.51659 12.59221
## uq max neval
## 333.69472 436.24961 100
## 14.20492 36.44741 100
## 12.70713 35.46495 100
## 14.18844 39.18424 100
## 12.69065 36.18741 100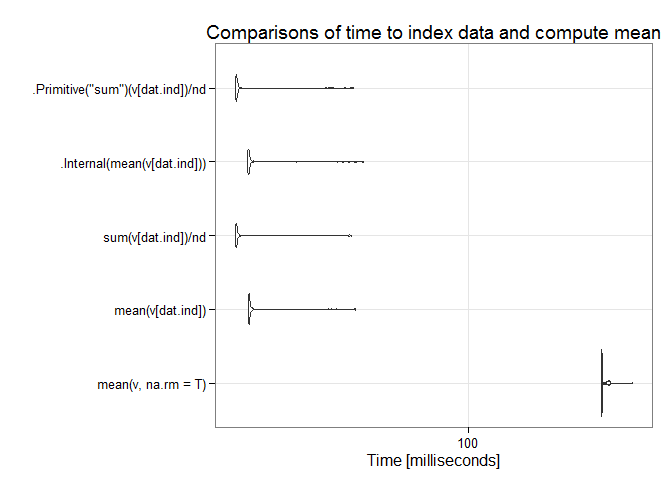
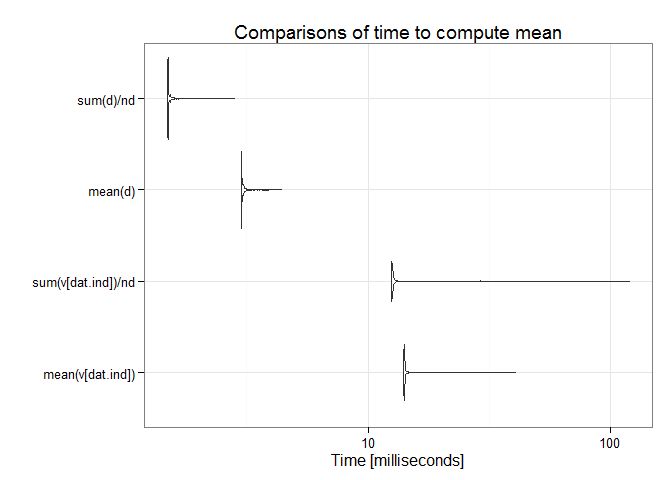
## Unit: milliseconds
## expr min lq mean median uq
## mean(v[dat.ind]) 13.940724 14.054862 15.692511 14.112709 14.212696
## sum(v[dat.ind])/nd 12.418051 12.527058 14.080500 12.576819 12.663589
## mean(d) 2.999005 3.010046 3.048648 3.018910 3.047055
## sum(d)/nd 1.495927 1.500281 1.526706 1.504635 1.514277
## max neval
## 40.684519 1000
## 120.171675 1000
## 4.425889 1000
## 2.837906 1000